令和の時代のカリキュラムデザイン　
[第1回]子どもの有能さを引き出す教師の仕事

島根県立大学教授　
齊藤一弥

（『新教育ライブラリ Premier II』Vol.1　2021年4月）

「個別最適」と「協働的」が意味すること

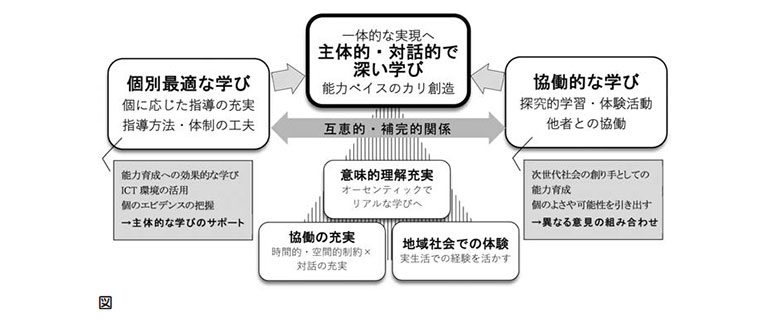
　今年1月末の中教審答申において2017年版学習指導要領の主旨の実現を目指した「令和の日本型学校教育」の方向性が示された。全ての子どもたちの可能性を引き出すためには「主体的・対話的で深い学び」の創造が不可欠であり、そのために「個別最適な学び」と「協働的な学び」を一体的に実現していくことが大切とされている（図参照）。これまでの日本型学校教育を発展させ、改めて「子どもの能力育成」に視点を当てて令和の時代の教育を切り拓いていくというものである。

　「個別最適な学び」と「協働的な学び」という対照的な学びの方法・形態が重視されているわけだが、なぜ両者がクローズアップされたのか、その意図を確認しておく必要がある。子どもはそもそも有能であって、その可能性をしっかりと引き出すためには、これまで以上に学びの質を高める必要があり、その具体的な改善の方向を2つの学びの在り方から検討していくということであろう。これまでも「個に応じた指導」の重要性は繰り返して話題にされ、指導方法や指導体制の工夫が行われてきたが、今回の「個別最適な学び」においては、主体的な学びをサポートするために個のエビデンスを正しく把握することやICT環境等の活用によって能力育成への効果的な学びを支援することが期待されている。一方、「協働的な学び」においては、個を埋没させることなく、そのよさや可能性を引き出しながら異なる意見を組み合わせて新たな価値の創造していくために、他者との対話を重ねながら探究的かつ体験的な活動を充実させていくことを重視している。

　そして、この2つの学びが互いに互恵的かつ補完的な関係を保ちながら、「主体的・対話的で深い学び」を実現していけるように、資質・能力ベイスの新たなカリキュラムをデザインしていくことが求められているわけである。

子どもの有能さを引き出すために必要なこと

　算数の授業をイメージしてみよう。これまでの多くの授業では、教科書の問題を形式的につかみ（課題把握）、問題解決を行って（自力解決）、全体で解決方法や結果を確認し（共同思考）、まとめと練習課題の処理をする（まとめ・適用）といった学習展開であった。

　しかし、両者の学びの実現によって、これまでの学習は内容的にも方法的にも大きく進化していくことが想定される。これまでにも増して子どもの有能さを引き出し、主体的・対話的で深い学びの実現を可能にするはずである。具体的に学びの様相がどのように変わるのかをみていこう。

見方・考え方を働かせる学びを描く

子どもは豊かな知識を有して学びに向かっている

　個別最適な学習環境や協働による対話の充実は、子どもの学びを主体的かつ自動詞的に動かし始める。生活や学習での経験を基盤にしたり既有の見方・考え方を働かせたりすることによって、子どもは必然性や切実性のあるオーセンティックでリアルな学習課題を設定していく。表1は5年生の「割合」の単元の導入場面である。3人がバスケットボールのシュートの上手さを競っている場面である。それぞれがシュートを放ち、シュートの入った回数が示されている。「これによって上手さは判断できるか」と問うと、子どもは「確かにCが一番シュートの入った回数は多いが、このままでは判断できない」と言う。比較量である「シュートの入った回数」だけで比較することはできず、基準量である「シュートの回数」が必要であると言う。つまり、「2つの数量の関係による割合によって判断する必要がある」という問題を、子ども自身が設定（「数学化」「問題設定」）していくことになる。子どもが学びに主体的になれるか否かは、このように問題がオーセンティックでリアルであるかどうかにかかっている。

　子どもは、実生活での様々な経験によって問題解決を支える豊かな知識や技能を有しており、それが数学的な見方・考え方となって学びを推し進めることになる。ある子どもに尋ねると、「シュート数を1としてシュートが入った回数の大きさで考える」と言う。既に無自覚的に身の回りの事象を割合として見ることで課題解決していることも多く、また、前学年で学習した「簡単な割合」での学びで獲得した知識がしっかりと活かされていることがわかる。身の回りの事象を割合として見ることで課題解決していることは多い。このような経験を想起させて、既有の知識等を丁寧に引き出しながら、他者との対話を通して算数の問題として自覚化させ、その内容（割合）の意味を実感的に理解していくことが大切であり、これによって見方・考え方が鍛えられていくことになる。個別最適な学びによって一人一人が自己の経験と対峙し、協働的な学びによってその経験の価値を共有するわけである。

オーセンティックな学びを実現する文脈や状況の組織

子どもは自ら文脈や状況を描き続けながら学び続ける

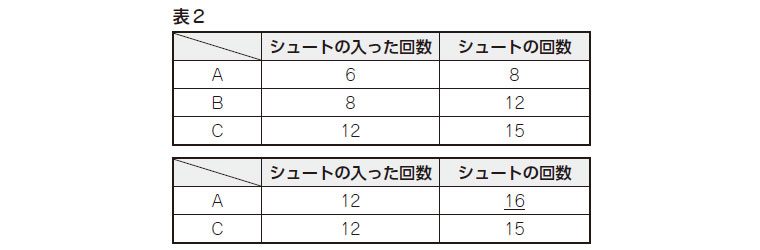
　問題が設定されたのを受けて、各自の自力解決に入るが、そこでの学びの状況は多様である。子どもの問題解決の方法は、それまでの学習経験によって支えられておりそれが反映されて表出される。表2上表に示された数量の関係からシュートの上手さを割合としてみた比較の仕方も多岐にわたる。

　まずは、シュートの入った回数がC（12）はA（6）の2倍のため、両者のシュートの入った回数を12回にそろえて比較することで、Cの方が上手いことがわかる（表2下表）。そこでBとCの比較をすればよいことがわかる。

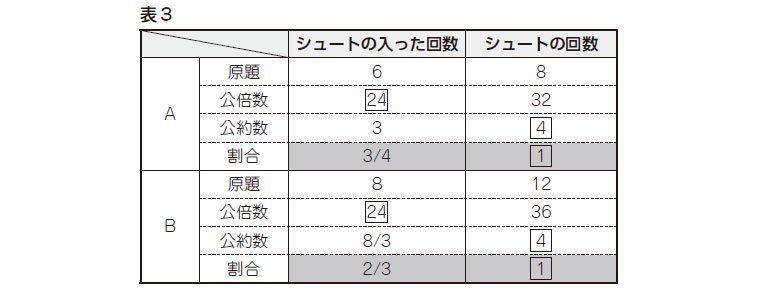
　次に、この両者を割合で比較すると、「シュートの回数を1とした時のシュートの入った回数の割合」「シュートの入った回数を1とした時のシュートの回数の割合」の方法が考えられる。また、既習の公倍数や公約数を活用することで「シュートの入った回数を24や2にそろえる」「シュートの回数を4や24にそろえる」などで解決することが想定される（表3）。

　これまでの授業においてもこのように多様な考えが出てきていた。その中から比較・検討に適した解決方法を選択して取り扱ってきたわけである。しかし、その背後で埋没している個々のアイデアが多かったのも事実である。このような場合、ICT（ロイロノートなど）の活用によって、教師は子どものエビデンスを瞬時に的確に把握することができるとともに、授業の文脈を状況に合わせてデザインすることができるようになる。また、子どもも集団全体に個々のアイデアを共有したり対話対象の範囲を拡大したりすることなどが容易になり、他者とともに学びの進む方向を確認していくことになる。また、個々の子どもが自分自身の解決方法の集団の中での位置付けや価値について確認することができるようにもなる。これまでは時間的・空間的な制約によって限られた数名の解決方法の比較という情報共有しかできなかったものが、指導の個別化によって効果的かつ効率的な比較・検討を可能にし、結果的に協働的な学びの質を高めていくことになるわけである。

　授業では、公倍数や公約数を用いて一方の数量をそろえて他方の数量で比較することに関心が高かった集団が、次第に割合の見方で比較することに関心を寄せるようになる。一方の数量を1とみた時の他方の数量の大きさ（「割合」）によって判断するものである。前学年での「簡単な割合」や同学年で学習した「商としての分数」で得た知識が結びついて、「シュートの回数」を1とした時の「シュートが入った回数」の大きさ（「割合」）を導き出すことはそれほど難しいことではない。ここでもICTの活用によって、子どもの解決方法への関心が「割合」を用いた方法へ次々と流れていく様子が共有され、他者との対話の効率化を図ることを可能にしていく。

学びの価値を自覚し次につなげる明示的指導の徹底

子どもは学びの価値を実感し、それを統合・発展させていく

　これまでの授業であれば、「割合」の意味とその用い方を理解してまとめた後で、適用問題に取り組んで終わるのが一般的であった。しかし、今回の学習指導要領の目指す算数の深い学びにおいては、学習の「振り返り」として「学習したことの価値を自覚して、次の学びにつなげていく」ことが期待されている。学びを振り返り、何ができるようになったかを問う「振り返り的省察」と、できるようになったことを用いると新たに何に取り組めるのかを問う「見通し的省察」との双方を繰り返して取り組むことが大切である。これまでの学びとの異同を確認しつつ、これまでの学びの成果と統合し、さらには新たな学びへ発展させていくことが期待されているわけである。

　授業の終盤には、「どの方法が便利でいつでも使えるか」という問いが設定された。これによって「割合」という内容が有する働きや用い方、よさについて考えるわけである。授業からつかんだ「割合」を用いることの価値を「公倍数や公約数を見出すのが難しいような数値でも簡単に除法で処理できる」「例えば、3つ、4つなどの複数の数量の関係を比較する場合も便利」などと提案し、ICTの活用によってその有用さがいくつかにグルーピングされて全体共有された。子どもが先人先達の文化遺産としての教科の内容の価値を見出し続けていったわけである。

　また、日常生活での経験からも「割合としてみる」で問題解決している場面が多いことが議論された。この学びの先には、「割合」に関して、個々の興味・関心や実体験などによって学習対象を見出し、それぞれに個別の課題解決をした後で、全体で比較・検討および共有するといった学習の個性化の場面をデザインすることも可能になるであろう。

　確かな学びに真摯に向き合おうとする子どもの有能さを引き出すためには、「個別最適な学び」と「協働的な学び」を一体的に充実させていくことが必要であろう。しかし、その新たな学びを実現するためには、新学習指導要領の主旨を反映したカリキュラムデザインが求められており、これからの学校そして教師には、その描き手としての力量が問われている。

[引用・参考文献]
●文部科学省「『令和の日本型学校教育』の構築を目指して〜全ての子供たちの可能性を引き出す、個別最適な学びと、協働的な学びの実現〜（答申）」（中教審第228号）、2021年1月26日
●齊藤一弥著『数学的な授業を創る』東洋館出版社、2021年

Profile
齊藤　一弥　さいとう・かずや
　横浜国立大学大学院修了。横浜市教育委員会首席指導主事、指導部指導主事室長、横浜市立小学校長を経て、平成29年度より高知県教育委員会事務局学力向上総括専門官、令和3年4月から高知県教育委員会事務局教育課程推進専門官。文部科学省中央教育審議会教育課程部会算数・数学ワーキンググループ委員。近著に『数学的な授業を創る』（東洋館出版社）。