授業力を鍛える新十二条

[第10回]対話の質を問い直す
第十条:〈授業コントロールの技〉―「明示的指導 対話」

島根県大学人間文化学部教授
高知県教育委員会事務局学力向上総括専門官　齊藤一弥

（『リーダーズ・ライブラリ』Vol.10　2019年2月）

対話の目的は、子ども同士の協働や教師との関わり、さらには先哲の考え方を手掛かりに考えること等を通じて、自己の考えを広げ深めることである。教科教育で身に付けるべき資質・能力の獲得に至るために、多様な表現によって教師と子ども、子ども同士が対話しながら、それによって思考を広げ深めていくことが求められる。形式的な対話からの脱却を目指し、対話の質を問い直すことが求められている。

対話的な学びが目指すこと

　次代の学びが重視する「主体的・対話的で深い学び」が目指すことは、これまで行われていた教師の実践に対する意図やこだわりや特定の指導方法を否定するものではない。「学び」という営みの本質を捉えながら、教師が教えることに丁寧に関わり、子どもたちに求められる資質・能力を育むために必要な学びの実現に向けて授業の工夫・改善を重ねていくことである。これまでの学びの在り様をしっかりと見つめ直し、何を、いかに変えていくべきかを見極めることが求められているわけである。

　指導方法を一定の型にはめてしまい、教育の質の改善のための取組が形式的な授業の方法や技術の改善に終始するのではないかと懸念されるようになって久しい。教育技術の改善を模索する意欲的な教師の営みがある一方で、授業づくりへの工夫や改善が本来の目的を見失ってしまい、学習指導の型に拘泥した状況が広がっているのも事実のように思える。

　中でも、対話の視点からみると、学習活動が指導の型をなぞるだけに終わってしまい、子どもの自主性に委ねると称した形態での活動によって対話が形式化して学びなしという状況に陥っている。本来、「対話的な学び」とは、子ども同士の協働、教職員や地域の人との対話、先哲の考え方を手掛かりに考えること等を通じて、自己の考えを広げ深めることを目指している。身に付けた知識や技能を定着させるとともに、物事の多面的で深い理解に至るために、多様な表現を試すことを通じて、教師と子ども、子ども同士が対話しながら、それによって思考を広げ深めていくことが求められるわけである。

形式的な対話からの脱却

　子どもの対話を重視した試みは、以下に示すような課題が多い。

　このような授業では、「対話的な学び」の目指す子どもの学びの姿を実現するのは難しい。確かに、これらは表面的には子どもが互いに関わり合って活発に発言し合う授業ではあるが、このような対話では子どもの成長を支えていくことにはならない。ここでの対話の質の違いを見極めることが肝要である。

　各教科における見方・考え方を働かせて、教科ならではの思考・表現が対話によって現出されることが期待されている。子どもがそれぞれの考えのよさや事柄の本質について対話することでよりよい考えに高めたり深めたりするなど、子どもが自分自身の変容を実感できるようにすることが欠かせない。

いかに対話を組織するか

　子どもが自他の考えを広げ、深めていくためには、対話の目的や方向性を彼らが意識していることが必要である。そうすることで、対話を通して新たな概念や思考や表現方法等を身に付けたり、深まりのある考えに変容したりすることにつながっていく。つまり、教師には子どもにとって価値ある学びになるようにその質を上げるための対話を組織することが期待されていて、授業ゴールを明確にし、その実現への文脈を描くことが必要である。

　小学校4年の算数の授業でその具体を紹介する。

　面積の導入で一辺が1mの単位正方形の普遍単位を導入する場面である。量を普遍単位で測ることについては、それまでに長さ、かさ、重さなどで既に経験している。大半の子どもは、先行経験によって1m²の単位の存在に気付いていたりすることから、多くの授業では教師が既習経験を土台にして指導事項としてそのものを提示するという展開になっている。つまり、普遍単位としての単位正方形については教師が教えるべきことであって、子どもが考えることではないとして子どもは何も考えることなく終わってしまう。つまり、授業にはならないわけである。

　もちろん、子どもに本来教師が教えるべきことである指導内容を議論させたり、その意味付けをさせたりする必要はない。一辺1mの正方形の1m²という普遍単位そのものも、先人の営みの中から生み出された文化遺産であるから、それの事実を知らせることは教師の仕事である。しかし、教科指導においては子どもに「教科という文化」が創られてきた過程に触れさせ、その働きや必要性、価値やよさなどを理解して、「教科という文化」を継承し、それを創造していくことの価値を経験させること、つまり、文化が創造されてきたプロセスを追体験しながら思考させていくための対話が大切なのである。

学びの質を高める「対話」への関心

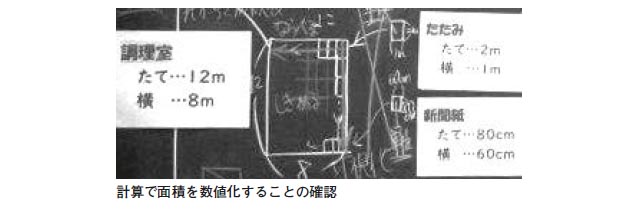
　授業では、学校の教室の広さを比較する場面が用意された。教室と調理室の面積を畳や新聞紙を敷き詰めて、その枚数で比較すれば大小判断ができるというのが子どもの考えである。その枚数をいかに調べたらよいかという課題である。

T1:「調理室はどんな形でしたか」
C1:「長方形です」
T2:「では、調理室になぜ新聞紙や畳を並べることができたのですか」
C2:「新聞紙も畳も調理室と同じ長方形だからです」
T3:「では他の図形だと並べることは無理ですか」
C3:「できなくはないけれども、長方形の方が並べやすい」
C4:「長方形だからこそ、調理室に全部新聞紙や畳を並べなくても敷きつめられる数がわかった」
C5:「縦に何枚並ぶかと、横に何枚並ぶかさえわかれば敷き詰めなくてもよかったよ」

　C4及びC5の発言にあるように、面積を畳や新聞紙などの任意単位で数値化する際には、測定対象の教室が長方形であることから、その形状の特徴を活かして乗法を適用することで簡便に求めることができることを明らかにしていった。

　さらに、縦や横に新聞紙や畳を敷きつめることをしなくても、何枚敷きつめられるかを求めることができることを追究しようとした。

T4:「次に縦と横に新聞紙や畳を並べなくても、それぞれ何枚敷きつめられるかがわかりませんか」
C6:「調理室の縦と横の長さをひもで測ればいい」
C7:「巻き尺で縦と横の長さを測った方がいいよ」
T5:「調理室の縦と横の長さを測るだけで、そこに全部で何枚敷きつめられるかがわかりますか」
C8:「調理室だけじゃなく、新聞紙や畳の縦と横の長さがわかるといい」
C9:「部屋の縦と横の長さを、新聞紙や畳の縦と横の長さでわれば、昨日のように調理室の縦と横に並べなくても何枚敷きつめられるかがわかるね」
C10:「縦と横に何枚を計算で求めることができる」

　C7からC10までの発言にあるように、任意単位が縦、横それぞれに何枚ずつ並ぶかを計算で求め、その枚数を用いて乗法によって面積を数値化することを確認した。一連の思考のプロセスを対話によって確認していったわけである。自他の考えを比べることによって自分のアイディアをより多様に膨らませていくことを対話が可能にしている。

　さらに、面積を求める単位を一辺が1mの正方形にすれば、長方形や正方形の辺の長さがそのまま各辺に並ぶ単位の個数となって、計算の手間が省けることも対話を通して明らかにしていった。

T6:「計算で求めれば、実際に新聞紙や畳を並べなくても何枚敷きつめられるかがわかりましたね」
C11:「でも、計算が面倒でした」
T7:「どうして面倒でしたか」
C12:「いつもわり算しないといけないので大変でした。もっと簡単なやり方があるはずだと思う」
T8:「じゃあ、わり算を使わなくても何枚分あるかわかる単位はどんな単位でしょうか」
C13:「÷1(1で割る)のだったら簡単」
C14:「1でわってもわり算の答えは変わらない」
C15:「全部1mだったら、わり算しなくていいよ」
C16:「そうだ。一辺の長さが1mの正方形を使うと簡単で、わり算しなくてよくなるよ」
C17:「それだったら、調理室の縦と横の長さを測ったときにもうわかるね」C18:「測った長さがそのまま使えるようになるね」
T9:「便利なことに気付いたみんなもすごいけど、これを発見した昔の人もすごいと思いませんか」

　ここでの対話の対象は先哲の知恵との対話である。

　C11からC12までの発言では、測定過程で実感した「計算の手間が面倒」であることを確認し、それを受けたT8の問いかけに対して、C13からC18までの子どもは労力を省くことのよさに関心をもって発言を続けている。普遍単位を創り出した先哲と実際に対話することはできないが、教師や子ども同士とが対話することで先哲の知恵に触れることになり、子どもたち自身で深い学びを創り出していくことになった。

　面積を数値化していく中で、簡潔かつ的確な方法への関心をもちながら数学を創っていくことは、教科という文化を創り上げてきた先人の知恵が生み出された過程を追体験していくことであり、子どもはそのよさを感じることとなった。教科を学ぶこととは、このように教科のもつ価値を子どもが実感することでもある。

対話の価値を問い直す

　子どもが問題場面に出合い、それと関わる中で何を考えるのか、どのように納得したり感じたりするのかを教師自身も実際に経験することで、子どもが対話の対象にすべきことが見えてくる。このようなプロセスを踏むことで、子どもと教師の対話、子どもが先哲の考え方を手掛かりに考えるべきこととが明らかになり、それを対話によって明示的に指導することで学びの質を高めることを可能にするわけである。

[参考文献]
・伊藤説朗・伊従寿雄編著『小学校算数科(4年)授業に生きる教材研究』明治図書、1982年
・横浜市立三ツ沢小学校編著『みんなが答を出せる算数の授業』明治図書、1985年

Profile
高知県教育委員会事務局学力向上総括専門官
齊藤一弥
さいとう・かずや
島根県立大学人間文化学部教授。東京都出身。横浜国立大学大学院教育学研究科修了。横浜市教育委員会授業改善支援課首席指導主事、指導部指導主事室長として「横浜版学習指導要領」策定、横浜型小中一貫教育の企画・推進などに取組む。平成24年度より横浜市立小学校長を経て、平成29年度より高知県教育委員会事務局学力向上総括専門官。30年10月より現職。文部科学省中央教育審議会教育課程部会算数・数学ワーキンググループ委員、小学校におけるカリキュラムマネジメントの在り方に関する検討会議協力者。主な著書に『「数学的に考える力」を育てる授業づくり』（東洋館出版社）、『算数 言語活動 実践アイディア集』（小学館）、『シリーズ学びの潮流4 しっかり教える授業・本気で任せる授業』（ぎょうせい）、『小学校教育課程実践講座・算数』（ぎょうせい）などがある。