授業力を鍛える新十二条

[第11回]見切りの繰り返しで学びを描く
第十一条:〈授業コントロールの技〉―「意思決定」

島根県大学人間文化学部教授
高知県教育委員会事務局学力向上総括専門官　齊藤一弥

（『リーダーズ・ライブラリ』Vol.11　2019年3月）

授業とは、子どもの意見で次々と違った様相を呈すものであり、教師は授業デザインを大切にしながらも子どもの状況を最優先に考えた不断の見切りを繰り返し、的確な意思決定をしながら次のステップを描き続けることが求められている。子どもの状況に合わせて適切にコントロールしながら授業を創っていかなければ、授業には子どもが不在となり、それは形式化、形骸化してしまう。

「子どもと授業を創る」という基本

　教師は誰のために授業を行っているのであろうか。改めて確認するまでもないが、それは子どものためである。では、授業の良し悪しは何によって判断されるのであろうか。それも子どもにとって価値があるかという点から判断される。このことに教師は誰もが納得する。つまり、目の前の子どもにとっての価値が授業診断の基準であり、その子どもの実態とその成長に合わせて授業も変容し質的に高まるべきであるということに異論はないはずである。

　日々の授業実践の成果は、少しずつではあるが着実に子どもに現れてくる。だからこそ教師は、子どもの実態を的確に見取って、それを基にしながら次の授業をデザインして、実践につなげていく。常に伸びようとしていて、日々成長していこうとする子どもの期待に応えるために、教師はよりよい授業を追い求めていくわけである。子どもとともに成長していくことは教師の責務と言える。

　しかし、子どもとともに授業を創るという当たり前を日々の実践で実現し続けることは決して容易なことではない。教師は授業の計画を重んじて、子どもの実態とは違ったストーリーを辿ってしまったり、授業の状況に関心をもちながらも自らを見切り子どものための授業の舵を切ることをためらったりすることが多いのではないだろうか。本来、授業とは子どもの置かれている状況によって常に教師が見切りと意思決定を繰り返して、最適な学びを描き続けることである。教師が自己の負うべき責任を回避し、子どもの実態を見捨ててあらかじめ決めていた方向に予定調和的に授業を進めたとき、子どもとともに創る授業とは程遠いものとなる。子どもの今と丁寧に関わりながら、子どもにとって有益な時間であったかを判断し続けていくことは、教師にとって欠かすことができない「技」だと言える。

子どもの見方・考え方を活かす意思決定

　筆者が高知県香美市立舟入小学校6年生で行った算数の実演授業を紹介する。これまでの学習で身に付けてきた図形の概念や性質を用いて、様々な場面での長さの測定方法を考えることを取り上げた。授業展開の概要と最終板書は次のとおりである。

①直接測定ができない問題場面を解決する

　手の届かない黒板の上の左端から右端までの長さは、黒板の下の左端から右端までの長さを測ればよいことを、長方形の性質を用いて説明する。

　次に、2点間の距離を測定する場合、巻き尺等を用いて測定するが、途中に障害物等がある場合はどうするかを考える。

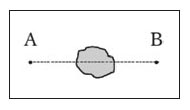
「直接測定ができない場合はどのように測定すればよいか」

②長方形を用いて測定方法を説明する

長方形の向かい合う2辺が等長であることを活用して、直接測定できない2点間の距離を測定することができることを説明する。

③より簡便かつ正確な方法を考える

「より簡単な方法で等しい長さを作れないか」

長方形の性質を使えば間接測定は可能になるが、直角を作ることの難しさと手間に関心をもつようにして、直角を用いることなく解決する方法はないかを問う。

既習の基本図形で確認した等長・等辺についての見方を活かす。

④巻き尺2本だけで等しい長さをもつ合同な三角形を描く

等しい長さについては基本図形の性質に加えて、合同、対称でも経験している。測定可能な場所に合同な三角形を描くことを考える。「合同な三角形で等しい長さを作ればいい」

対応する辺の長さが等しいことを用いて、2点間の距離と等しい長さが作れることを説明する。

⑤場面が変わっても、縮図・拡大図の概念を活用して学び続ける

「三角形を描いたスペースにも障害物があったらどうするか」

例えば、合同な三角形を描くスペースがなかったらどうしたらよいかと条件を変えながら問い続ける。

限られたスペースに縮図を描いて間接測定を試みる。

点Aから点Bまでを直接測定ができない場合、長方形を描いて対応する辺の長さが等しい性質を用いて測定すればよいことを確認した(②)後で、直角を用いることなくより簡便に測定する方法を考える(③)場面である。

T12:直角を作るのに手間がかかって難しいということでしたが、三角定規の直角を使わずに等しい長さを作ることはできないでしょうか。これまでの学習で等しい長さをもつ図形の学習をしたことはありませんでしたか。

C16:正方形で…とか。

C17:それも直角を使っている。

C18:正三角形を描けば、点Aから点Bまでの長さがわかる。

T13:確かに正三角形は等しい辺をもった図形ですね。でも、正三角形はどのように描きますか。

C19:辺ABと60度になる直線を点Aと点Bから2本の直線を引いて、その線が交わると正三角形ができる。それを点Cとして点Aから点Cまでの長さが点Aから点Bまでの長さと等しくなる。

T14:直角は使っていないけれど、角度を使っていて、手間がかかり面倒ではありませんか。

C20:60度のある三角定規を使えばすぐにできる。

T15:実際に床で試してみましょう。(実際に作業した後で…)直角を作ったときと同じような感じがしますが…。先程は長方形を作りましたが、今度は正三角形を作って考えたわけですね。

C21:点Cとして点Aから点Cまでの長さが点Aから点Bまでの長さと等しくなる。

C22:三角形を他に場所に描いてもいい…。

T16:確かに別の場所に等しい長さを作ることができました。この正三角形を見て、床には等しい長さをもつ図形が見えてきませんか。

C23:三角形の逆にもう一つ三角形を描けばいいのかな。

C24:同じ形の三角形をかけばわかる。そして対応する辺の長さを測ればいい。

T17:同じ形とは…。

C25:合同な三角形を作る…。

T18:正三角形を用いた方法から、また合同な三角形を作るという別の方法を考え出すことができました。

　子どもは、それまでに経験したことを発展的、創造的に見つめ直して、新しい視点から学び続ける。つまり、自分のもつ数学的な見方・考え方を総動員して、それを拠り所にして物事を思考したり、判断したりした先に、新たな見方・考え方を上乗せしていく。新たな経験知をこれまでの経験知といかにつなげていくかを考え、教科ならではの見方・考え方を成立させていくことになる。

　一方、教師は、子どもから表出される見方・考え方に、子どもの新たな学びの可能性を見出すことになる。

　「等しい長さをもつ図形」を想起させる問いかけ(T12)によって、子どもは辺が等長の図形に関心をもってしまった。教師は、合同な図形の対向する辺を想起させようとしたが、その思惑とは異なる方向へ子どもの思考は動いていった。授業の計画段階では想定されなかった正三角形を利用するという反応(C18)は、教師の見切りを要求するとともに新たな意思決定を求めてきた。正三角形を床に描くことで、そこから合同な三角形を見出すという新たな授業場面(T16)を構成し直すことを、その場で瞬時に描いていくことになった。

　当初計画していた「長方形の性質の利用から合同な三角形の性質の利用への思考のプロセス」は、子どもだけでイメージすることはかなり難しいと考えていた。しかし、正三角形の性質を利用した方法を取り上げたことで、三角形を活用することへの関心が高まり(C22、C23)、結果的には子ども自身が合同な三角形の性質を利用すること(C24)に目を向けるようになった。

　藤岡完治が「『教える』ということは、授業という子どもとの相互性において成立する場において、教師が用意した教育内容に子どもがしっかりと応え、さらに潜んでいる可能性を発揮するのを手助けする営みである」と言うように、子どもの今と丁寧に関わりながら、子どもに必要な学びの文脈を描くための意思決定をすること、それを支えるための徹底した教材分析が教師に期待されていることがわかる。

見切りの不断の繰り返しによる授業デザイン

　授業とは、子どもの意見で次々と違った様相を呈すものであり、教師はそれらを受けて、的確な意思決定をしながら次のステップを描き続けることが求められている。確かに教師が授業デザインを大切にしながらもそれに固執することなく、子どもの現状を見極めて新たな展開を用意するのは、ある意味果敢なる決断である。しかし、上田薫も指摘するように、授業とは、または教師の指導とは目の前にいる子どもの状況を最優先に考えた見切りの不断の繰り返しであり、教師はこの見切りによって新たな目標や方向を意思決定し、見切ることによって目の前の子どもに主体的な学びを保証していく必要がある。

　つまり、教材分析も授業デザインも子どものために行われているものであり、そこにいる子どもの状況に合わせて授業を創っていく姿勢を大切にして、授業を適切にコントロールしていかなければ、授業には子どもが不在となり、それは形式化、形骸化してしまうからである。

[参考文献]
・藤岡完治著『関わることへの意思教育の根源』国土社、2000年
・重松鷹泰・上田薫・八田昭平編著『授業分析の理論と実際』黎明書房、1963年

Profile
高知県教育委員会事務局学力向上総括専門官
齊藤一弥
さいとう・かずや
島根県立大学人間文化学部教授。東京都出身。横浜国立大学大学院教育学研究科修了。横浜市教育委員会授業改善支援課首席指導主事、指導部指導主事室長として「横浜版学習指導要領」策定、横浜型小中一貫教育の企画・推進などに取組む。平成24年度より横浜市立小学校長を経て、平成29年度より高知県教育委員会事務局学力向上総括専門官。30年10月より現職。文部科学省中央教育審議会教育課程部会算数・数学ワーキンググループ委員、小学校におけるカリキュラムマネジメントの在り方に関する検討会議協力者。主な著書に『「数学的に考える力」を育てる授業づくり』（東洋館出版社）、『算数 言語活動 実践アイディア集』（小学館）、『シリーズ学びの潮流4 しっかり教える授業・本気で任せる授業』（ぎょうせい）、『小学校教育課程実践講座・算数』（ぎょうせい）などがある。