
授業力を鍛える新十二条
授業力を鍛える新十二条[第8回]見方・考え方と学びの文脈 第八条:〈授業コントロールの技〉―「文脈の生起」
トピック教育課題
2019.11.07
授業力を鍛える新十二条
[第8回]見方・考え方と学びの文脈
第八条:〈授業コントロールの技〉―「文脈の生起」
島根県大学人間文化学部教授
高知県教育委員会事務局学力向上総括専門官 齊藤一弥
新教育課程が目指す三つの柱の資質・能力の育成に向けた授業づくりには、見方・考え方を基軸に据えて授業の文脈を描くことが大切である。学びの対象への着眼と対象との関わりを子どもが自覚的に行えるように教師が子どもと文脈を生起していくことが期待されている。
「見方・考え方」を働かせた授業へ

これまでの連載の中で、教科の本質を確実に学ぶために「見方・考え方」は不可欠であり、教科指導の土台を支えているものであること、また、その「見方・考え方」を子どもが働かせながら学ぶには、真正で本物の教科学習の場を用意することや先人先達の文化継承としての教科の役割を意識することが大切であり、それによって子ども自らが教科の価値に出合い、それを実感的に納得することを確認してきた。
「見方・考え方」を働かせるとは、表面上異なった対象への関わり方、アプローチの仕方、そしてそれらを支えるアイディアの裏側のそれぞれに共通するものの存在に気付きながら学ぶことであり、その結果として、子どもは個々の事実や知識を統合・包括する概念や教科ならではの認識や表現の方法などに関心をもつとともに、一段抽象度の高い概念や思考を獲得していくわけである。「見方・考え方」を基軸に据えて、これまでの学びの在り様を見つめ直していくことが求められている。
「見方・考え方」の見極めと授業への位置付け
横浜市立小学校に勤務する採用3年目のY先生は、小学校算数の5年で「四角形の内角の和が360°になることを筋道立てて説明すること」を扱う場面を授業提案することになり、その指導展開の相談を受けたときのことである。
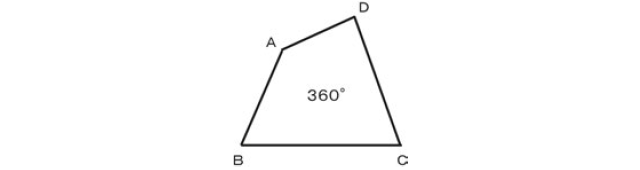
Y先生は、学習指導案を作成するにあたり学習指導要領や解説を丁寧に読み込み、三角形や四角形などの多角形の簡単な性質として内角の和を理解するとともに、その性質を用いて内角の和を筋道立てて考えたり説明したりすることが求められていることを確認した。また、四角形の内角の和の求め方を形式的に理解することで終わるのではなく、内角の和を求める際に論理的に思考することの大切さなど、この図形学習をすることを通してどのような資質・能力を身に付けていくべきかを考える必要があることも理解していた。
しかし、このように丁寧に教材分析をしても、算数・数学らしい学びの文脈をうまく描くことは難しかった。この学習で必要とされる「三角形の内角の和が180°であること」や「角という量には加法性があること」、さらに「四角形は対角線や補助線で複数の三角形に分割されること」などといった既習事項を子どもが活用しながら、いかに演繹的に思考しながら学び進んでいくのかを見通せないでいたのである。これまでの経験から、子どもに既習経験を想起させ、それを踏まえて教科固有の知識を習得するだけであれば単位時間の流れをイメージはできる。しかし、それでは論理的思考の育成を目指す授業には程遠い。ここから抜け出すためにはどうしたらよいのであろうか。
授業には身に付ける資質・能力の獲得という目指すべきゴールがあるが、それに辿り着く文脈は能力ベイスの授業のねらいや目標、子どもの実態や状況によっても多様かつ複雑である。決して画一的でパターン化されたものではない。しかし、その一方で学びづくりの基本として押さえるべきことはあるはずである。この授業で言えば、数学的な資質・能力の育成に向けて数学的活動をいかに組織するかが肝要であり、その数学的活動は子どもが潜在的に有している数学的な見方・考え方を働かせるプロセスととらえることができる。このことは、小学校学習指導要領の算数の教科目標の柱書きにある「数学的な見方・考え方を働かせ、数学的活動を通して、数学的に考える資質・能力を育成する」ことを逆に読み解くことで見えてくる。つまり、算数・数学らしい学びの文脈を描くには、この学習で必要とされる数学的な見方・考え方を見極めた上で、それをいかに数学的活動に位置付けるかを考えていくことが必要なことが分かる。
「小学校学習指導要領解説 算数編」より一部抜粋
図形の性質を筋道を立てて考え説明すること
筋道を立てて考えることには、ある前提を基に説明していくという演繹的な考えが代表的なものである。帰納的な考えや類推的な考えもまた、根拠となる事柄を示すという点で、筋道を立てた考えの一つといえる。(中略)三角形の三つの角の大きさの和が180度であることが分かると、それを基に発展的に考え、四角形の四つの角の大きさの和はどうなるかを考えることができる。四角形の四つの角の大きさの和は、三角形の三つの角の大きさの和が180度であることを基にして考えることができる。このように、既に正しいことが明らかになっている事柄を基にして別の新しい事柄を説明していくことを演繹的に考えるという。(以下略)



















