
学び手を育てる対話力
学び手を育てる対話力[第3回]わからなさから学びを生み出す対話力
トピック教育課題
2019.10.03
学び手を育てる対話力
[第3回]わからなさから学びを生み出す対話力
東海国語教育を学ぶ会顧問 石井順治
対話的学びで姿を現すわからなさ
わからなさから学びが生まれます。ところが、学校にも社会にも、わかることが優秀でわからないことは劣っているという価値観があり、子どもたちはわからなさを表に出すことができないでいます。それはよいことではありません。わからなさを安心して出せる教室にする、それはすべての子どもの学びを深める鍵です。
中学校2年数学の授業、この時間の課題は以下のようになっていました。
弟が9時に自転車で家を出発し、一直線の道路を図書館に向かった。姉は、弟が家を出発してから7分後に自転車で家を出発し、弟と同じ道路を図書館に向かった。2人は途中でそれぞれ1回ずつ自転車を止めて休み、9時39分に同 時に図書館に着いた。図は、9時x分における弟と姉の間の距離をym としてx、yの関係をグラフに表したものである。
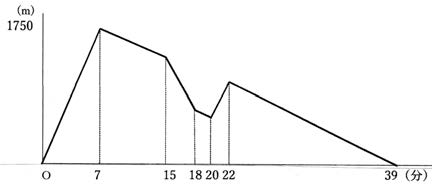
ただし、弟と姉の自転車の速さはそれぞれ一定であり、2人がそれぞれ1回ずつ自転車を止めて休んだ時間に重なりはないものとする。
(平成21年度三重県立高等学校入学者選抜学力検査問題)
この文章の後に、姉が図書館に着くまでに走った時間、家と図書館との距離、9時20分における弟と姉の距離という3つの問いが出されていました。
課題が出るとすぐグループになる、この学校の授業のいつもの光景です。最初のグループでわからなさが出る、それもいつものことです。この授業でも当たり前のように出てきたのですが、そこには思いもかけないわからなさと間違いが含まれていました。
「1750って何?」
「このグラフって、弟のこと表してるの?姉のことを表したもの?」
「(xが7のところでyが1750になっている点について)ここが図書館や」
「(xが39のところでyが0になっているその点を指差して)家に帰って来た!」
教師からすれば途方に暮れるような状況ですが、数学の苦手な子どもの方こそこういうところで先に進めずもっと途方に暮れているのです。
これらのわからなさや間違いはグラフの直線を何分でどれだけの距離を走ったかを表していると見てしまったことから起こっています。だから、グラフの直線は弟なのか姉なのかという質問が出てきたのだし、直線の山のいちばん高い1750のところがいちばん遠いところだと感じ、そこが図書館だと錯覚してしまったのです。「1750って何?」という疑問も、そこが図書館ではと感じたのだけれど、問題には姉が7分後に出発したと書いてあり、そこが1750になっている、一体どういうことだろうとわからなくなったのでしょう。また、39分のところで家に帰り着いたと考えたのも距離が「0」になっているので家に帰ってきたと思ってしまったのです。
つまり、これらの子どもは「ともなって変わるx、yの関係」という関数的見方ができないでいるのです。たぶんこの子どもたちも、x、yに何らかの数字を代入してグラフにするという関数の学習はしてきているのでしょう。しかし、具体的状況になると途端にわからなくなるのです。ここを乗り越えないと一次関数は理解できないし、実生活でこの課題のような考え方をすることはできません。
そういう意味で、こういうわからなさが表に出せるのは素晴らしいことなのです。教師の説明で進める一斉指導型の授業だとこういうわからなさや間違いは出て来ません。出せる場がないし、授業がわかっている子どもの発表で進むからです。その発表の陰でつまずいている子どもは、いつまでもこうしたわからなさを抱えることになるのです。
それが、この学級ではあたり前のように出てきます。そして、どのグループでも他の子どもたちが実に丁寧に温かく対応しています。なぜでしょうか。
それは、数学の授業ではもちろん、どの教科の授業でも常にグループになって対話的学びをしているからです。どんな間違いもわからなさも大切に受け止め合い、そこからすべての子どもの学びを生み出す学びを日常的にしているからです。
ただし、このようなわからなさや間違いも、学びとして昇華させることができなければ深い学びは実現できません。対話的学びの良さや大切さを実感することもありません。それにはこの授業の場合どういうことが必要なのでしょうか。
乗り越えるための足場を

こういうとき必要なのは足場です。足場は子どもだけではかけられないことが多く、どのようにかけるにしても教師がかかわります。もちろん教師が説明してわからせるということではありません。適切な足場をかけ、その足場をもとに子どもたちで乗り越えていけるようにするのです。例えば次のように。
まず2人の子どもが考えていた「何分でどれだけの距離走ったかを表す」という考え方を否定しないで、小学校の算数の授業で描いていたような数直線(下図参照)にしてみてはどうでしょうか。
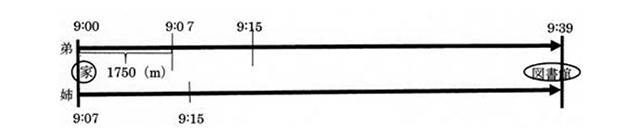
そのうえでこの数直線と課題の一次関数のグラフとを比べてどこがどう異なるのかグループで考え合うよう仕向けるのです。そうすれば間違いは生き、表し方の違いも見つけ出せ、関数的な見方にも正面から向き合うことになるのではないでしょうか。そしてわからなさを抱えていた子どもだけでなく、どの子どもの学びをも深めることにつながります。
できないこと・わからないことを克服してきたのが人間の歴史だとすると、日々の授業におけるわからなさはささやか過ぎるかもしれません。けれども挑む価値に違いはないのではないでしょうか。学びはわからなさから始まります。対話的学びはそのわからなさを引き出し深めます。
Profile
東海国語教育を学ぶ会顧問
石井順治
いしい・じゅんじ 1943年生まれ。三重県内の小学校で主に国語教育の実践に取り組み、「国語教育を学ぶ会」の事務局長、会長を歴任。四日市市内の小中学校の校長を務め2003年退職。その後は各地の学校を訪問し授業の共同研究を行うとともに、「東海国語教育を学ぶ会」顧問を務め、「授業づくり・学校づくりセミナー」の開催に尽力。著書に、『学びの素顔』(世織書房)、『教師の話し方・聴き方』(ぎょうせい)など。



















