確かな思考を保障する文脈を子どもとともに描く

　四角形の内角の大きさの和を求める際に、既習の三角形の内角の大きさの和を活用していかに問題解決するかが授業づくりのポイントになる。ここでは三角形の内角の和（180°）という知識を基にして、三角形や四角形の構成要素に着目して、図形の性質から四角形の内角の和の求め方を多面的に考察することが期待されている。具体的には、四角形を対角線や補助線で複数の三角形に分割し、そのいずれの場合においても、内角の和が360°になることを演繹的に説明するというゴールまでの学びの文脈を子どもとともに描いていくことになる。

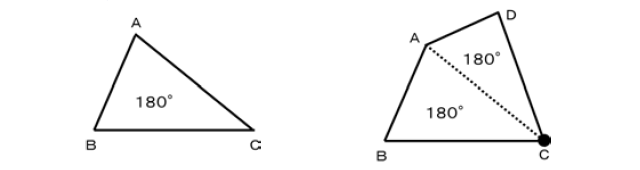
　右図のように点Ｃから点Ａに向けて対角線を引き２つの三角形に分割すると、次の式で四角形の内角の和を簡単に求めることができる。

〇２つの三角形の内角の和⇔180°×2＝360°

　確かにこれだけでも演繹的に考えたことにはなるが、これでは単位時間の授業は成立しないため、Ｙ先生は子供に自力解決させて、その解決方法を取り上げて共同思考する展開をイメージしていた。つまり、個々にいろいろな分割方法に自由にチャレンジさせて、その方法を全体で確認して共有するという展開であった。問題解決のプロセスの型としてはオーソドックスではあるが、それだけでは必ずしも演繹的に思考することに自覚的に取り組むことにはならずに悩んでいたわけである。

　そこで次のような学びの文脈を提案した。対角線で２つの三角形に分割する方法で四角形の内角の和が360°であることを確認した後に、下図のように点Ｃから辺上に移動させた点Ｅから２つの頂点に向かって補助線を引いて、３つの三角形から四角形の内角の大きさの和を求めるという文脈を子どもとともに描き、次のように全体で考え進む展開を用意する。

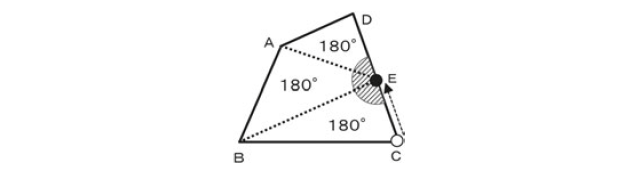
〇補助線の引き方が変わって３つの三角形ができるので、その内角の和を合わせると180°×3＝540°⇔「360°にならないけどいいのだろうか」
【構成要素への着目、演繹的思考による一応結果の吟味、数学的な問い】

〇辺上の点Ｅの周りにできている角が余分⇔「これは四角形の頂点の角ではない」辺上の点Ｅの周りの角の大きさは180°⇔「直線または２直角なので180°」３つの三角形の内角の和を合わせた角の大きさから180°を引く⇔「180°×3－180°＝360°となり四角形の内角の大きさになる」
【構成要素への着目、一応の答えが誤っていることの理由を演繹的に説明】

　２つの三角形に分割して内角の大きさを求める方法との違いを意識しながら、事象を丁寧に観察することを通して、思考結果のずれ（360°にならないこと）の理由を説明するわけである。本来は子ども自らがこのように演繹的に考え、それを的確に表現してほしいわけだが、全ての子どもにこのような文脈を自ら描くことを期待するのは難しい。演繹的に考えることやそのために構成要素やその関係に着眼することには慣れていないからである。ましてや360°になる理由を簡潔・明瞭かつ的確に説明するとなるとかなりハードルが高くなる。教師に期待されているのは、子どもにこのように演繹的に考えて、表現する経験を積ませることである。つまり、教師が子どもとともに文脈を描きながら、数学的な見方・考え方を働かせて数学的活動を進めていく経験を積ませることが大切になる。教師が「範」を示して、それを子どもに「なぞらせる」ことから始めてもよいであろう。このような場を設定して、子どもに論理的な思考の進め方を学ばせるようにすることが求められている。「子どもは何も教えなくてもどんどん学べる」と誤って無責任に自力解決の場に放り出してはいないだろうか。子どもは自らの経験に支えられてのみ学び進むわけだから、先に示したようなプロセスの中で演繹的に考えながら、思考結果の誤りの理由を説明するという経験を繰り返していくことが必要である。