
講座 単元を創る
講座 単元を創る[第5回]「縦」と「横」を意識した単元づくり 見方・考え方の成長の連続を意識する
授業づくりと評価
2019.12.18
講座 単元を創る
[第5回]「縦」と「横」を意識した単元づくり 見方・考え方の成長の連続を意識する
島根県立大学教授
高知県教育委員会事務局学力向上総括専門官
齊藤一弥
■summary■
これまでの単元づくりを問い直し、見方・考え方を基盤とした系統や関連を再確認して、その成長をささえる学びを描くことが大切である。子供が見方・考え方を積極的に働かせていけるように学びの「縦」と「横」の関連を意識した単元を描くことが期待されている。
見方・考え方の成長を意識した単元の在り方

資質・能力ベイスの授業では、子供自らが見方・考え方を働かせて学びを切り拓いていくことが期待されている。このことは、子供に学習内容を見方・考え方でつなぐことやその関連に関心をもてるようにするために、見方・考え方で単元間の関係や関連を見つめ直すことが必要なことを意味している。これまでの単元を問い直し、その系統や関連を再確認して学びを描くことで、子供の見方・考え方はさらに鍛えられ、成長していくことが可能になり、その結果として身に付ける資質・能力を獲得していくことになる。
見方・考え方の成長を「縦」につなぐ

例えば、中学校数学の「数と式」領域の方程式の学習では、第1学年で「一元一次方程式」、第2学年で「連立二元一次方程式」、そして、第3学年で「二次方程式」を学んでいく。子供がそれぞれの学習で身に付けた見方・考え方を働かせながら、内容のつながりを意識しながら学び進んでいくことになる。各単元においては、「方程式を解くとはどのようなことをしているのか」と確認しながら、数量の関係に着目するとともに解決方法を統合的に捉えていくことを繰り返していくことが大切である。
そこでは、一次方程式で確認した「文字は1つで等式の形になれば解は決まる」ことを基にして、「文字を1つにするためにはどのようにすればよいか」という視点から見方・考え方を働かせて学び進んでいくことになる。一元一次方程式の解決方法の延長線上に、連立二元一次方程式、そして二次方程式の解決方法を見出していくことができれば、「多くの解決方法を覚えなくても、同じ見方・考え方で問題を解決することができる」と解決方法の価値やよさを実感しながら確かな理解を図ることができる。
しかし、ここまでくると中学校までの学習経験にも関心をもつことが必要であることが分かる。先述のとおり「一元一次方程式」は、等式の性質(左辺と右辺の同値な関係を保ちながら目的に応じて式変形をして最終的にx=kの形にすること)によって解を求めるわけだが、この性質の理解には、小学校で鍛えられてきた見方・考え方が働くことが期待される。次の図のように、小学校では計算の性質を理解するために、式と式の関係を見たり同値な関係に着目したりするなどして数量の関係についての見方・考え方を育ててきているが、これらが土台となって等式の性質の理解をするとともに、その性質を利用して一元一次方程式の解き方を見出していくことになる。
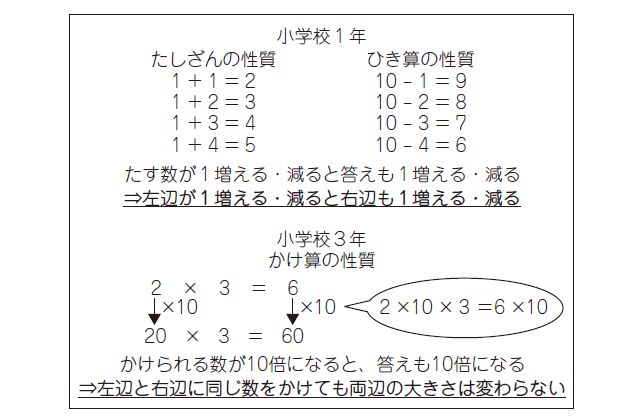
このように学年を越えて単元で育成する見方・考え方を「縦」に確実につないでいくことが重要であり、子供は見方・考え方を働かせることで知識や技能のそれぞれがバラバラなものではなく、関連したもの、そして統合されたものとして認識するようになり、資質・能力を支える体系化された概念として身に付いていくことになる。
見方・考え方の成長を「横」で支える

二元一次方程式では、ax+by+c=0は未知数を求める式として捉えるが、同学年で学習する「関数」領域の一次関数においては、それを2つの変数xとyの間の関係を表した式として捉える見方を扱っている。二元一次方程式のxとyの数量関係に着目すると、「xの値が決まればyの値がただ1つ決まる」という関数的な見方を育成するわけである。また、一次関数においては、二元一次方程式のxとyの解の集合を座標平面上の点の集合(これが直線になる)として捉えることも扱う。一次関数と連立二元一次方程式の学習とを関連付けることで、改めて方程式の解の意味を捉え直し、より深く理解することを可能にする。座標平面上に示された二直線の交点が、連立二元一次方程式の解としても求められることを、一次関数のグラフを用いて考察することによって連立方程式の解の意味を視覚的に捉えることができる。

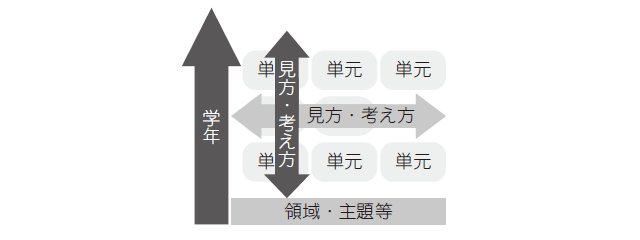
このようにして、一次関数で育成された見方・考え方が、連立二元一次方程式の学習内容を深く理解することになるわけだが、見方・考え方の成長には、同じ領域の内容を積み上げていくことはもちろんであるが、関連する内容を扱う単元の「横」の関係をも意識しながら単元を描くことも重要であることが分かる。
見方・考え方という視点から学びの「縦」と「横」の関連を意識した単元を描くことで、子供は学びから得た見方・考え方を働かせながら学び続けることができるようになる。子供が自らの見方・考え方という経験知に開かれた学びを可能にするために、改めて単元間の在り方を捉え直すことが期待されている。
[引用・参考文献]
•齊藤一弥・高知県教育委員会編著『新教育課程を活かす能力ベイスの授業づくり』ぎょうせい、2019年
Profile
島根県立大学教授
高知県教育委員会事務局学力向上総括専門官
齊藤一弥
さいとう・かずや
横浜国立大学大学院修了。横浜市教育委員会首席指導主事、指導部指導主事室長、横浜市立小学校長を経て、29年度より高知県教育委員会事務局学力向上総括専門官、30年10月より現職。文部科学省中央教育審議会教育課程部会算数・数学ワーキンググループ委員。近著に『新教育課程を活かす能力ベイスの授業づくり』。



















