講座　単元を創る
[第10回]見方・考え方の成長と校種間関連

島根県立大学教授
高知県教育委員会事務局学力向上総括専門官
齊藤一弥

（『学校教育・実践ライブラリ』Vol.10 2020年2月）

■summary■
校種を越えて学び続けている子供に対応するために校種間の関連を意識した単元を描くことが大切である。子供が身に付けてきた見方・考え方を働かせながら学びをつなげていくための単元デザインへの転換が期待されている。

子供を主体に据えた校種間連携をイメージする

　子供は小学校での学びを活かしながら、中学校での豊かな学びを実現する。このような学びを実現するためには、双方の学習指導要領の主旨理解を徹底し、校種間の接続をいかに捉えたらよいのかを確認し、それを授業の具体につないでいくことが求められる。

　中学校1年数学の「図形の移動」の指導は、小学校算数の「対称な形」の内容と関わりとを意識した指導によって子供の学びの連続を可能にする。小学校6年での「対称な形」の学習を受けて、中学校1年では図形の移動を通して図形間の対称性を考察することになるが、対称移動と線対称、回転移動と点対称との両者のつながりはもちろんのこと、小学校低学年の図形指導との関連も意識しながら指導を連続させていくことが重要である。

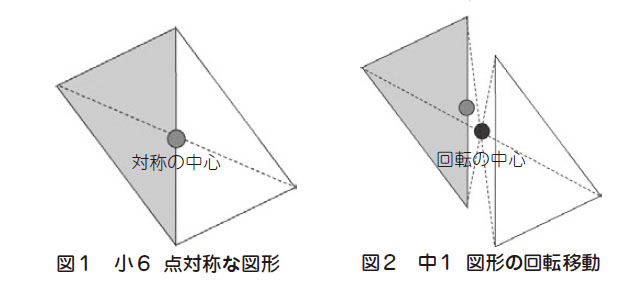
　具体的な場面で考えてみる。点対称な形の作図では、対称形の半分(灰色部分)を示して残りの半分（白色部分）を対称性を活用して作図するが（図1参照）、対称の中心の位置を変えても形を描くことができる（図2参照）。対称の中心を図形の外側に移動させることで、点対称の図形の作図と図形の回転移動との間に関連が見えてくるが、それぞれの校種ごとで別々に指導されているため、子供はそれらを独立したものと捉えて、関連付けることはなかなか難しい。小学校で学んだことを統合的・発展的に捉えて問題解決に活かすには格好の場面のはずである。条件を変えた場面で、それまでに鍛えてきた見方・考え方を働かせて課題解決することは大切であり、それによって子供が主体的に学習に取り組むようになるチャンスを見逃している。

　このことを解決するためには、先を見越した単元づくりが必要であり、小学校の単元づくりにはその先の中学校を意識して学びを開いておくこと、中学校の単元づくりではそれまでの小学校での学びをきっかけにつなぎを丁寧に組み立てることが欠かせない。つまり、これまで以上に双方の学習の関連を意識していかに単元を描くかが鍵になる。

見方・考え方の成長からみる校種間関連の在り方

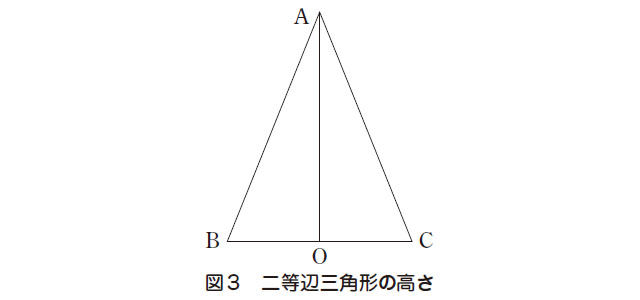
　高知市立三里中学校で行われた数学科の授業研究では、生徒の見方・考え方の成長を踏まえた単元づくりが話題になった。授業は中学校1年の平面図形の学習で垂直二等分線の作図の仕方を学ぶ場面である。それまでの指導では、作図の手続きを確認して、それを用いて適用問題を解決するという流れであったが、子供が見方・考え方を働かせて作図方法を考えていくために、「二等辺三角形の高さを決める」(図3参照)という課題を用意した。三角定規や分度器などを用いずに、点Aから底辺BCと点Oで垂直に交わる直線AOをどのように引いたらよいかというものである。

　学習指導要領解説には、小学校までに学習してきた「等辺・等長」「対称性」といった概念を活かしながら作図を行うことが示されている（下抜粋参照）。つまり、図形の等辺や対称性に関心をもちながら、これまでの基本図形の性質や関係を活かして作図に取り組むことが期待されている。この前提を踏まえながら学びを描くためには、単元を通してどのような見方・考え方を働かせればよいのかが問われていることになる。

　授業では、二等辺三角形の高さとなる点Aから底辺BCへの垂線を引くために、まず初めに点Bと点Cから等長の点Dを決めた。次に、点A、点B、点C、点Dを結んで四辺相等のひし形を作る。さらに点Aと点Dを結んで、底辺BCとの交点までを高さとした。

　この一連の作図の過程において、子供にはどのような見方・考え方を働かせることが期待されているのであろうか。授業後の研究会では、小学校の算数科での学びとの関連に関心が集まった。4年の内容の「ひし形の性質(四辺相等、対角線が直交し二等分される)」や6年の内容の「線対称の性質(対応する点を結ぶ線分は対称の軸と垂直に交わり二等分される)」、さらには直近の中学1年の内容の「対称移動の性質」など、いずれも「対称性」に関わる内容が作図を支えているということである。これらが「直線AOが二等辺三角形ABCの高さ」になっていることの根拠であり、それを子供自らが解決に向けて用いていくことが必要となるわけである（図4参照）。

　授業研究会に参加していた教師の多くは、図形の性質は覚えることがゴールではなく、それを活用して問題解決していくことに価値があることを再認識するとともに、校種を越えたそれまでの学びの連続性を再確認すること、さらには見方・考え方の成長との関連を意識した単元を描くことの必要性などを実感することになった。

学習指導要領解説　中学校数学編（一部抜粋）
基本的な作図
図をかくという操作は、図形に対する興味や関心を引き起こし、図形の性質や関係を直観的に捉え、その論理的な考察を促すという意義をもつ。
数学において作図とは、定規とコンパスだけを用いて、一定の条件を満たす図形をつくることを意味し、定規は2点を通る直線をひく道具として使い、コンパスは円をかいたり長さを写し取ったりする道具として使う。基本的な作図では、小学校算数科で学習した平面図形の対称性に着目して、角の二等分線、線分の垂直二等分線、垂線などについて学習する。このとき、作図の方法を一方的に与えるのではなく、図形の対称性や図形を決定する要素に着目して作図の方法を見いだし、その方法を図形の性質や関係に基づいて説明する活動を大切にする。（以下略）

Profile
島根県立大学教授
高知県教育委員会事務局学力向上総括専門官
齊藤一弥
さいとう・かずや
横浜国立大学大学院修了。横浜市教育委員会首席指導主事、指導部指導主事室長、横浜市立小学校長を経て、29年度より高知県教育委員会事務局学力向上総括専門官、30年10月より現職。文部科学省中央教育審議会教育課程部会算数・数学ワーキンググループ委員。近著に『新教育課程を活かす能力ベイスの授業づくり』。