第１章　コンピテンシー・ベイスという思想
５　学習の転移は簡単には生じない

上智大学教授
奈須正裕

（次代の学びを創る知恵とワザ）

優れた問題解決者を育てるコンテンツ・ベイスの論理

　ここまで、従来型の教育が抱える問題点をあれこれと見てきたけれど、実はコンテンツ・ベイスの教育も子どもを「歩く百科事典」にしようとしたわけじゃない。コンピテンシー・ベイスの教育と同様に、子どもを優れた問題解決者にまで育て上げることを目指していたと、僕は考えている。

　だって、そうだろう。親も教師も、さらには社会だって、子どもの頭をコンテンツの缶詰にすればいいなんて思うはずがないじゃないか。当然、子どもたちの社会的成功、人間的成長、よりよい社会創造への貢献を願ってきたに違いない。そしてそのためには、人生の中で出合う数々の困難、そこでの多種多様な問題解決に際し、自分はもとより多様な他者にとって少しでも望ましい解決を粘り強く多角的に模索し、現に成し遂げられるようになることが大切だって、誰しも考えるだろう。

　では、コンテンツ・ベイスとコンピテンシー・ベイスの分かれ目はどこにあるかというと、この教育の原理的な課題というか目標をどのような筋道で達成できると考えるか、その違いにあると僕は思う。

　コンテンツ・ベイスの教育では、それが文化遺産として遺された普遍的に価値ある知識や技能の選りすぐりを習得させることで可能になると考えてきた。なぜなら、学問・科学・芸術といった文化遺産は、永い歴史の中で人類が成し遂げてきたもっとも偉大にして洗練された革新的問題解決の成果として、そこで新たに生み出された知識や技能が後生に遺され、集成し体系化されたものにほかならない。ならば、そういった知識や技能を子どもに習得させておけば、先々彼らはそれらを適宜上手に活用し、同様の優れた問題解決を成し遂げながら人生を生きていくだろうって期待したんだよ。

　すると、カリキュラムや授業づくりの戦略としては、各文化遺産の体系に照らして重要と思われる知識や技能の選りすぐりを、基礎からはじめてできる限り高度なものまで数多く正確に教えることが基本方針となる。いうまでもなく、これこそが教科の成り立ちであり、編成原理ということになる。

　このような論理を背景に持つからこそ、コンテンツ・ベイスの教育はその成果を確認するのに「何を知っているか」を問うことで事足れりとしてこられた。つまり、「何を知っているか」それ自体にも十分に価値はあるんだけど、さらにそのことがほぼ自動的に「どのような問題解決を現に成し遂げるか」を保障し、ひいてはその子の将来における社会的成功や人間的成長、よりよい社会の創造を予測すると信じてきた。だからこそ、領域固有知識の教授と習得状況の確認が学校と教師にとって最大の関心事であり、力の入れどころでもあり続けてきたんだ。

　この論理が事実に照らしてあやしいことは、１－３で紹介した、コンテンツ・テストの成績が人生の成功を予測しないというマクレランドの研究からもすでに明らかなんだけど、ここではさらに別な角度から考えてみたい。

実質陶冶と形式陶冶

　誰しも、子どもに教えた領域固有な知識や技能それ自体がその領域の学習や問題解決に直接的、特殊的に効果や有用性を持つ、この考え方を「実質陶冶」っていうんだけど、この実質陶冶は至極当然のこととして、さらに学びの成果が他の領域にも拡がり、生きて働いてほしいと願っているだろう。

　たとえば、数学はその知識の習得に際し、子どもに厳密な形式論理的思考を要求する。すると、その過程では論理性や思考力が培われ、それらは図形や数量以外の、それこそ政治や経済のような社会的事象の構造的理解や批判的思考にも礎を提供するんじゃないかと考えたくなる。実際、数学を将来において直接的に必要とはしない文科系の高校生にも必修とする根拠として、同様の論理はしばしば持ち出されてきた。この理屈でもって先生に説得され、心のどこかでは「なんかおかしいなあ」と思いつつも、しぶしぶ勉強をがんばったって経験のある人は少なくないんじゃないかなあ。

　このような、領域固有知識それ自体は仮に有用性が低くとも、その学習を通して思考力や創造性など汎用性のある資質や能力が鍛えられ、ひいては当初の狭い領域を超えて幅広い分野の学習や問題解決の質を高めるという考え方を「形式陶冶」という。

　もう、おわかりだろう。「何を知っているか」がほぼ自動的に「どのような問題解決を現に成し遂げるか」を保障するというコンテンツ・ベイスの教育の論理は、この形式陶冶の考え方を暗黙の前提に据え、頼りにしてきたんだ。

　形式陶冶の歴史は、古代ギリシャにまで遡る。人々は重いバーベルが筋力を鍛えるように、算術や幾何学などの難解な学問を修めることが一般的な知能と推論能力を高めると考えた。文字通りの「頭の体操」なんだけど、同様の主張は歴史上何度も繰り返し唱導されてきている。たとえば、少し前にも脳科学の専門家がこんなことを書いているのに出くわした。

　「脳も、手足の筋肉とまったく同じです。毎日、ランニングするのと同じように、計算問題を解き続けると、脳のいろいろな場所が活発に働くようになります。すると、脳のいろいろな場所がきたえられます。たくましい脳になると、脳をうまく使うことができて、いろいろな、もっとむずかしい問題を解くときも、じょうずに解けるようになるのです」１

［注］１　川島隆太『自分の脳を自分で育てる』くもん出版、二〇〇一年、二一頁

　新しい装いによる形式陶冶論であり、その論理は紀元前と何ら変わるところがない。少し前に流行った百マス計算や古典文学の暗唱など、読み書き算の機械的反復を正当化するのに、この「脳も筋肉」という論法が常套的に用いられているのは、すでにみなさんもお気付きの通りだ。

　古代ギリシャで生まれた形式陶冶論は、その後ヨーロッパの人々に受け継がれていく。彼らは一八世紀までに、文法、論理学、ラテン語、ギリシャ語などを形式陶冶に資する学問のリストに追加して拡充させ、その影響は二〇世紀に至るまで根強いものがあった。今でも、イギリスの名門進学校のことをグラマー・スクールっていうだろう。あれは、ラテン語のグラマー、つまり文法を教える学校、文法学校っていう意味なんだ。

　もっとも、中世ヨーロッパで最初の大学が生まれた一二世紀からしばらくの間は、大学の講義はすべてラテン語で行うのが普通だったから、ラテン語の学力はそれこそ実質陶冶的に不可欠だった。ところが、次第にそれぞれの国の母語で大学の授業がなされるようになっても、高等教育を受けるにはラテン語が必要だとされ続けた。

　ラテン語やギリシャ語はすべてのヨーロッパ言語の源であり、また言語は学問の基礎だから、ラテン語やギリシャ語の学習はヨーロッパで成立したすべての学問を効果的に習得する礎をなすと考えられたんだ。これは典型的な形式陶冶論といっていい。それくらい、形式陶冶の考え方は教育の世界で力を持ってきたし、今だって結構な力をもち続けている。そして、この流れの先に今日の教科を中心とした学校教育、つまりコンテンツ・ベイスの教育も位置付く。

学習の転移と教育測定運動

　しかし、形式陶冶論は事実に照らしてどこまで正しいのか。脳はどこまで筋肉であり、頭の体操はどれほどの有効性を持っているんだろう。

　これは、心理学でいう学習の「転移」に関わる問題になってくる。学習の転移というのは、先行する学習と後続する学習の間で生じる、何らかの影響の及ぼしあいを指す言葉だ。たとえば、中高での英語学習は大学でのフランス語やドイツ語の学習を促進し、一定量の学習を節約する効果をもたらす。たしかにそういった効果はあるけれど、では、その規模なり範囲はいったいどのくらいのものなのか。あるいは、似たような知識を学んだがゆえに、かえって以前の学習が混乱してしまう、つまり後続の学習が先行する学習を損なうような転移、これを負の転移というんだけど、そういう複雑なことだって起こりうる。

　このように、転移は学習や教育の価値なり効用に関わる重大な問題なんだけど、ギリシャ時代以来、人々は永年にわたって特に明確な証拠もなく、促進的な学習の転移が比較的容易に、また広範囲にわたって生じると信じてきた。

　これに対し、二〇世紀初頭のアメリカで、数量的な科学的実証を持って教育に関する意思決定を行うべきだとする教育測定運動が起こる。その中心人物だったソーンダイクは、学習の転移を暗黙の前提とする形式陶冶論にも十分な科学的証拠がないことに気付き、その検証に乗り出す。

　形式陶冶論が正しければ、ラテン語を習得した生徒は他の教科をより速く学習できるはずなんだけど、検証の結果、そのような証拠は何一つ見出されなかった。この結果は形式陶冶論を否定するものであり、信じられてきたほどには学習の転移が容易に、また広範囲にわたって生じはしないということを指し示している。

　もっとも、同時にソーンダイクは、二つの学習内容が類似している場合には、ある程度学習の転移が生じることを報告してもいる。彼は転移がもたらす学習の節約効果は、学習内容相互の類似性に依存すると考えた。実際、英語学習が第二外国語の学習にもたらす転移の効果は、単語や文法など多くの類似点を持つフランス語においてより高く、類似点が少ない中国語やロシア語では低いだろう。そう考えれば、ラテン語の学習が語学以外の教科の学習に促進効果をもたなかったことも、十分に納得がいくんじゃないかなあ。

Ａ問題とＢ問題の落差の原因

　学習の転移を巡る論争は、その後もさまざまな角度から精力的に進められた。そこでは実に多様な議論や発見があったんだけど、非常に大雑把にまとめるならば、心理学は一九七〇年代までには転移はそうそう簡単には生じないし、その範囲も限定的で、少なくとも何かしらの知識や技能を習得してさえいれば、それが有用な場面に出合うと常に自動的に発動され、問題解決なり学習を推進してくれるといったことはおよそ期待できないというあたりに落ち着いている。

　このことは二〇〇七年、文部科学省が四三年ぶりに実施した全国規模の学力テスト、全国学力・学習状況調査におけるＡ問題とＢ問題の成績の間に示された、圧倒的なまでの落差というか乖離からも明らかだ。

　たとえば、同じ平行四辺形の面積に関する知識を適切に用いれば正答できる問題であるにもかかわらず、授業で教わった通りの尋ねられ方をするＡ問題の正答率が九六％だったのに対し、図形が地図中に埋め込まれたＢ問題では、一気に一八％まで低下した（図１‐１）。

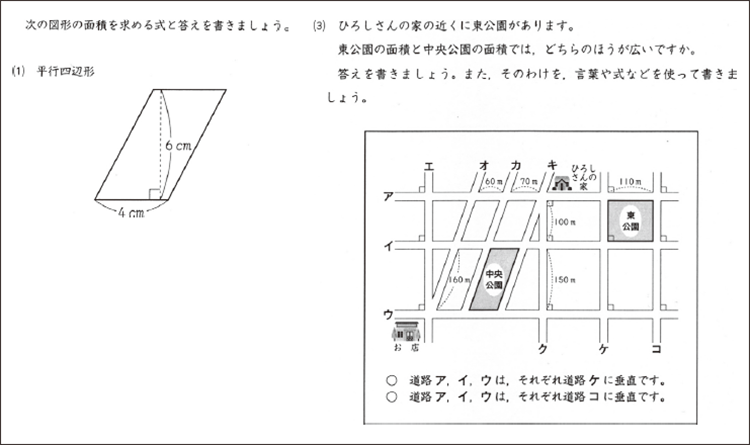
図１‐１ ６年生算数のＡ問題（左）とＢ問題（右）（2007 年度全国学力・学習状況調査）正答率：Ａ問題 96％、Ｂ問題 18％

　当時、この結果に驚きを隠せなかった人が多かったように記憶しているけれど、すると人々は、転移は割と簡単に生じるし、その範囲も結構広いと考えていたに違いない。でも、この間の研究結果が示唆する通り、Ｂ問題の低迷ぶりは当然の帰結であり、特に驚くような出来事ではないんだ。

　さらには、Ａ問題的な質でなされた学習がＢ問題的な水準にすら十分には転移しないことを考える時、数学学習が論理性や思考力を鍛えるという例の常套句についても、慎重に向かい合う必要がある。

　たしかに、数学学習は数量や図形を扱う上での論理性や思考力を高めるだろう。でも、同じことがどこまでの拡がりを持つのか。たとえば、僕の周りにも数学の専門家は何人もいるけれど、彼らが二四時間、すべての生活領域において論理的に思考して暮らしているかというと、う〜ん、まあ人それぞれかなあ。少なくとも数学的事象以外の対象の取り扱いに関して、数学を専門としない人々との間に、残念ながら格段の違いを僕は実感しないんだ。

　つまるところ、「何を知っているか」がほぼ自動的に「どのような問題解決を現に成し遂げるか」を保障するという、コンテンツ・ベイスの教育が暗黙裏に前提としてきたような無制限・無限定な学習の転移は、カリキュラムや授業づくりがよって立つ基盤とするには、やや脆弱に過ぎるということなんじゃないかと僕は思う。そして、たとえ意に沿わなかったり都合がわるかったりしたとしても、事実に即さない予断は、捨て去るなり修正するしかないだろう。

　ここで、「いや、Ａ問題ができれば十分なんだ」と言うのなら、もちろんコンテンツ・ベイスのままでも構わないけれど、そういう人は子どもの頭をコンテンツの缶詰にすればいいと思っているに違いない。かくいう僕は、すべての子どもを優れた問題解決者にまで育て上げたいと念じている、つまり、教育の目標に対する考え方がすっかり異なるから、そういう人とはこれ以上の議論は不可能ということになる。さて、あなたはどうしますか。

奈須正裕（なす・まさひろ）
上智大学総合人間科学部教育学科教授。博士（教育学）。1961年徳島県生まれ。徳島大学教育学部卒、東京学芸大学大学院、東京大学大学院修了。神奈川大学助教授、国立教育研究所室長、立教大学教授などを経て現職。中央教育審議会初等中等教育分科会教育課程部会会長。主な著書に『子どもと創る授業』（ぎょうせい）、『「資質・能力」と学びのメカニズム』（東洋館出版社）、など。編著に『新しい学びの潮流（全５巻）』（ぎょうせい）、『教科の本質から迫るコンピテンシー・ベイスの授業づくり』（図書文化社）、『教科の本質を見据えたコンピテンシー・ベイスの授業づくりガイドブック』（明治図書）など。