授業力を鍛える新十二条

［第７回］校種間のバトンを滑らかにつなぐ
第七条：〈単元づくりを支える勘どころ〉―「校種間連携」

高知県教育委員会事務局学力向上総括専門官　齊藤一弥

（『リーダーズ・ライブラリ』Vol.7　2018年10月）

子どもは校種を超えて学び続けているという当たり前に対応するためには、校種間連携を意識しながら学習指導要領を丁寧に読み解くことが必要になる。子どもが身に付けてきた見方・考え方を働かせながら学びをつなげていくために、子どもを主体にした単元デザインへの転換が期待されている。

子どもは学び続けるという当たり前の確認

　Ａ市が行った調査によると、小中学校の児童生徒へ「算数・数学の学習が好きか」と質問すると、学年が上がるにつれて肯定的な回答が少なくなり、小学校６年生の算数と中学校１年生の数学とを比較するとその割合が急激に減少している。これは、いわゆる「中１ギャップ」という現象を物語る一例であるが、その背景には算数から数学への滑らかな接続が難しいという実態がある。小学校算数での学びを活かし、さらに広げ、深めていくために、中学校数学の指導内容とのつながりを意識して、算数の出口を広げたり、または少し先に延ばしたりして、内容の接続を意識した指導が求められているが、算数で鍛えたはずの見方・考え方を、数学で十分に活かすことができていないのが現状である。その原因として、小中学校の教師が、算数と数学を通した見方・考え方を働かせた数学的活動の在り方を互いに意識しながら一貫した指導に結び付けることができていないことが挙げられる。

　子どもは小学校での学びを活かしながら、中学校での学びに期待をしている。その期待に応えるためには、双方の学習指導要領を丁寧に読み合うことで、校種間の接続をいかに捉えたらよいのかを確認し、それを授業の具体につないでいくことが欠かせない。前号で取り上げた小学校算数の「対称な形」の指導についても、その内容と関わりのある中学校１年の数学の「図形の移動」との接続を意識した指導をすることで児童生徒の学びの連続を可能にする。

　中学校数学の解説書に指導内容として上記のように示されている。小学校６年での対称な形の学習を受けて、中学校１年では図形の移動から図形間の対称性を考察することになるが、対称移動と線対称、回転移動と点対称との両者のつながりはもちろんのこと、小学校低学年の図形指導との関連も意識しながら指導を連続させていくことが重要であることが分かる。改めて言うまでもなく、小学校算数の授業づくりにはその先の中学校での学びを、中学校数学の授業づくりにはそれまでの小学校での学びを意識していくことが欠かせない。つまり、双方の学習指導要領を丁寧に読み合うことが求められているということである。

　しかし、現状はどうであろうか。小学校の指導を進める際に中学校の指導内容まで確認することは稀で、このような学習指導要領との付き合い方はしていない。子どもは小学校、そして中学校へと校種を越えて学び続けていくにもかかわらず、教師が校種を越えた授業づくりへの意識をもたないでいいのであろうか。

校種間連携とは、子どもを主体に単元を創るということ

　高知県香美市立香北中学校での筆者の実演授業の様子を紹介する。授業は次のような考えで構想された。

　中学校数学の「図形の回転移動」の導入で、小学校算数の「対称な形」の学習内容と関連させて「対称の中心」の位置を変えた場合の作図方法を考えることとした。これは、子どもが点対称の図形の性質や作図方法の学習を通して育んできた見方・考え方を働かせて中学校数学の「図形移動」の学習に取り組むことを重視した展開である。

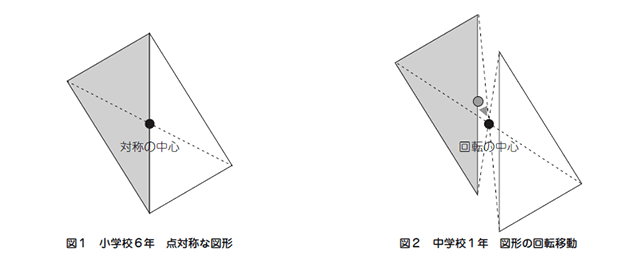
　「点対称な形」の作図では、対称形の半分（灰色部分）を示しておき、残りの半分（白色部分）を図形の対称の性質を活用して作図する（図１）が、対称の中心の位置を変えても形を描くこと（図２）ができる。図形の外側に対称の中心を移動させることで、点対称の図形の作図と図形の回転移動とを関連させながら学ぶことができるわけである。互いに関連ある内容であるにもかかわらず、それらが校種をまたいで別々に指導されているため、子どもはそれらを独立したものと捉えて関連付けることはなかなか難しい。小学校で学んだことを統合的・発展的に捉えて問題解決に活かすことを経験させるためには格好の場面である。条件を変えた場面で、それまでに学んだことを活かして課題解決することは、極めて重要であり、それによって数学的な見方・考え方を鍛えていくことになる。

　第１の課題では、平行四辺形を対角線で二等分した三角形１枚を提示して、残りの半分をかいて点対称な図形を完成させる。ここでは、点対称な図形の作図の方法を振り返り、対応する点を結ぶ直線が対称の中心で二等分されるという性質を活用したことを確認する。

　次に、第２の課題では、対称の中心が図形の外にずれたときでも、それを中心として回転させて作図することが可能かどうかを問う。第１の課題と関連させながら、条件が変わった場合でも、同じような作図が可能かどうかを考える。子どもが学び進んできた過程を重視しながら、新たな内容について滑らかに学習することができるように単元を描き直して新たな展開を用意した。

　授業の実際は次のとおりである。

　第１の課題で点対称の形の作図方法を確認したのちに、第２の課題として点対称の形の対称の中心の位置をずらし、そこを中心として180°回転させた三角形を作図することが可能かを考えることとした。

T18：対称の中心は三角形の辺上にありましたが、その場所を三角形の外側に動かしたとき、点対称の形と同じように180°回転した三角形をかくことはできそうですか。

C29：外側にずらすとは……。

T19：点Ｏの位置をずらしてみます。（実際に点Ｏの位置を外側にずらして見せる）

C30：そのようにずらすわけか……。でも図のかき方は同じだからできるのではないか。

C31：点対称な形のかき方で（作図を）すればいいわけかな……。

C32：②で確認した中心で対応する点を線は二等分されるという約束を使えばいいのではないか。

T20：その方法を使って、実際に書いてみましょう。（自力解決：作図）

　対称の中心Ｏがずれても、その点Ｏを中心にして三角形を180°回転させた図形を作図することができることを確認するとともに、そのプロセスを箇条書きで整理した。次に示すのが各項目のポイントである。

　第２の課題の作図を可能にする根拠は、点対称な形の「対応する点を結ぶ直線が対称の中心で二等分される」という性質であり、①および②はこれを活用していることを表している。

T23：Ａさんが説明してくれた作図の方法と点対称な形のかき方と比べてみて気が付いたことはありますか。

C35：どちらの方法も書き方が同じ。点対称な形の場合は①と②が点Ｂの場合だけを考えればよかったので簡単で済んだだけ。

C36：三角形は外側に離れたけれど、やっていることは同じということ。

T24：点対称な形のかき方で（作図を）すればいいということかな……。

C37：対称の中心と回転の中心とで変わったけれど、やっていることは同じ。

T25：皆さんが作図した図形の移動のことを点対称な形の移動と同じことなので、点対称移動ともいいます。やっていることが同じということに気が付いたことはとてもいいことです。

C38：小学校での対称な形の学習がつながっているということ……。

T26：これまで学んだことを活かせば簡単に考えることができるということですね。今の課題は180°の回転移動でしたが、その半分の90°回転移動の場合も作図できるでしょうか。（中略）

C43：Ｋさんの説明でも、①と③での90°を作るところは違うけれども、残りの②と④の作図方法は似ている。

T30：回転の中心をもとに図形を90°回転移動させる方法とこれまでの学習内容とつながって見えたということですね。

　数学的に内容がつながっていても、指導に連続性がなければ学び手の子どもにはそのつながりが見えてこない。小学校での既習内容を想起させ、さらには課題の提示の仕方や指導方法を工夫することで、それまで身に付けてきた数学的な見方・考え方を積極的に働かせ、子どもが学びの連続性に関心をもって取り組むことができた。小学校での学びを活かすことで、中学校の学びを実感的に受け止めて滑らかな接続を可能にすることになった。

　校種間の滑らかな接続を図ることで、子どもの学びが大きく変わっていくことがわかる。単元づくりは子どもを主体に置き、子どもと教師がともに描いていくという原点がここにあり、教師にはそれを形にしていく勘どころが求められている。

［引用文献］
・齊藤一弥共編著『シリーズ学びの潮流4 しっかり教える授業・本気で任せる授業』ぎょうせい、2014年、pp.65-126
・文部科学省『中学校学習指導要領（平成29年告示）解説　数学編』2017年

Profile
高知県教育委員会事務局学力向上総括専門官
齊藤一弥
さいとう・かずや　東京都出身。横浜国立大学大学院教育学研究科修了。横浜市教育委員会授業改善支援課首席指導主事、指導部指導主事室長として「横浜版学習指導要領」策定、横浜型小中一貫教育の企画・推進などに取り組む。平成24年度より横浜市立小学校長を経て平成29年度より現職。文部科学省中央教育審議会教育課程部会算数・数学ワーキンググループ委員、小学校におけるカリキュラム・マネジメントの在り方に関する検討会議協力者。主な編・著書に『「数学的に考える力」を育てる授業づくり』（東洋館出版社）、『算数 言語活動 実践アイディア集』（小学館）、『シリーズ学びの潮流4 しっかり教える授業・本気で任せる授業』（ぎょうせい）、『平成29年改訂　小学校教育課程実践講座　算数』（ぎょうせい）などがある。